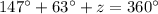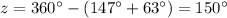Answer:
The measure of the third arc is
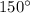
Step-by-step explanation:
step 1
we know that
The measurement of the external angle is the semi-difference of the arcs which comprises
in this problem
Let
x----> the greater arc of the circle intercepted by the secant and the tangent
y----> the smaller arc of the circle intercepted by the secant and the tangent
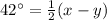
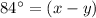 ----> equation A
----> equation A
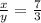
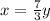 -----> equation B
-----> equation B
Substitute equation B in equation A and solve for y
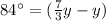
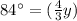
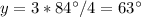
Find the value of x
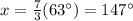
step 2
Find the measure of the third arc
Let
z------> the measure of the third arc
we know that
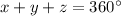 -----> complete circle
-----> complete circle
substitute the values and solve for z