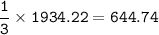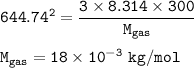Question

if an unknown gas has one third the root mean squarevspeed of H2 at 300 K, what is the molar mass of the gas?​

Answer 1

The molar mass of the gas : 18 x 10⁻³ kg/mol

Further explanation

Given

An unknown gas has one third the root mean square speed of H2 at 300 K

Required

the molar mass of the gas

Solution

Average velocities of gases can be expressed as root-mean-square (V rms)

`\large {\boxed {\bold {v_ {rms} = \sqrt {\frac {3RT} {Mm}}}}`

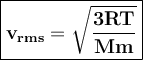
T = temperature, Mm = molar mass of the gas particles , kg/mol

R = gas constant 8,314 J / mol K

v rms An unknown gas = 1/3 v rms H₂

v rms H₂ :

`\tt v_(rms)=\sqrt{(3* 8.314* 300)/(2.10^(-3)) }\\\\v_(rms)=1934.22`

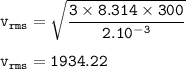
V rms of unknown gas =

`\tt (1)/(3)* 1934.22=644.74`

`\tt 644.74^2=(3* 8.314* 300)/(M_(gas))\\\\M_(gas)=18* 10^(-3)~kg/mol`