Answer:
D
Explanation:
According to remainder theorem, you can know the remainder of these polynomials if you plug in x = -6 into them.
So we will plug in -6 into x of all the polynomials ( A through D) and see which one equals -3.
For A:

For B:
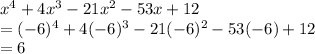
For C:
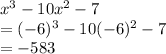
For D:
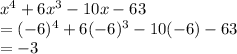
The only function that has a remainder of -3 when divided by x + 6 is the fourth one, answer choice D.