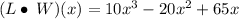ANSWER
Step-by-step explanation
The length of a rectangle is represented by the function:
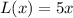
and the width is represented by
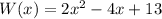
The area of a rectangle is calculated using the formula:
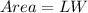
In terms x, we have
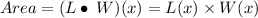
We plug in the functions representing the length and width to obtain;
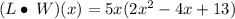
We expand the parenthesis to obtain;