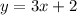Answer:
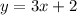
Explanation:
Given : The given line passes through the points (0,-3) and (2,3).
To Find: What is the equation, in point-slope form, of the line that is parallel to the given line and passes through the point (-1,-1)?
Solution:
Points : (0,-3) and (2,3).
To find the equation of given points we will use two point slope form
Formula :
 --A
--A
Where m is the slope
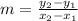
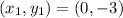
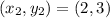
So,

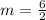

Now substitute the values in A
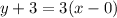
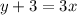
Two lines are said to be parallel when they have same slope
So, The line parallel to the given line will have slope =3
General form of equation of line =
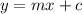
Substitute m = 3
So, parallel line :
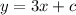 ---B
---B
Now this parallel lines passes through point (-1,-1)
So, substitute this point in B
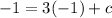

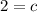
Substitute value of c in B
So, Equation of parallel line =
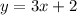
Hence the equation, in point-slope form, of the line that is parallel to the given line and passes through the point (-1,-1) is