Answer:
11.2 sq.ft.
Explanation:
We are given the window is in the shape of a regular octagon.
The radius of the window, including the frame, is 2 ft.
The measure of each edge of the octagonal frame is 1.52 ft.
Since the diagonals of regular octagon divides into 8 equal triangles
Two radii and one side forms one triangle.
We are supposed to find the approximate area of the window that needs to be covered, including the frame
Area of window including frame = Area of 8 triangles
So, first we need to find the area of 1 small triangle.
Heron's formula
Area of triangle =
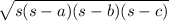
where a ,b and c are the sides of triangle
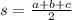
Substitute
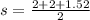
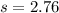
So, Area of triangle =
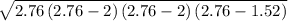
Area of triangle =
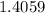
Area of 8 equal triangles =
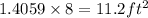
So, Area of window including frame=11.2 sq.ft.
Hence the approximate area of the window that needs to be covered, including the frame is 11.2 sq.ft.