Answer:
The draw in the attached figure
Explanation:
Let
L-----> the length of the rectangle
W----> the width of the rectangle
we know that
The perimeter of a rectangle is equal to
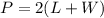
we have
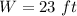
so
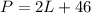 -----> equation A
-----> equation A
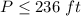 ----> inequality B
----> inequality B
substitute equation A in the inequality B and solve for L
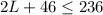
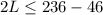

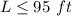
The maximum possible value of L is 95 ft
therefore
The rectangle could be
Length 95 ft
Width 23 ft
see the attached figure to see the draw