Answer:

Explanation:
If the triangle is a right triangle, then the sides will check out in the Pythagorean Theorem.

Where a and b are the legs and c is the hypotenuse.
1. Define Sides
The legs are the 2 shorter sides and the hypotenuse is the longest.
The sides given are 3, 4 (shorter), and 5 (longest). Therefore:
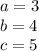
2. Check the Sides in the Theorem
Substitute the values into the theorem.
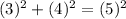
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Addition, and Subtraction.
Solve all of the exponents first.

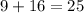
Add the numbers on the left side of the equation.

This is true. 25 is equal to 25, so this triangle can be a right triangle.