Question

The lengths of the sides of a triangle are 3, 4, 5. Can the triangle be a right angle. Yes. No.

Answer 1

Yes

Explanation:

3 , 4 & 5 are Pythagorean Triplet numbers. When lengths of a triangle's 3 sides are Pythagorean Triplet , the triangle is a right angled triangle.

The triangle will be a right angled triangle only when the hypotenuse will have length of 5 and other 2 sides will have length of either 3 or 4.

Answer 2

`\boxed {\boxed {\sf Yes, \ the \ side \ lengths \ 3, \ 4, \ and \ 5\ can \ make \ a \ right \ triangle}}`

Explanation:

If the triangle is a right triangle, then the sides will check out in the Pythagorean Theorem.

`a^2+b^2=c^2`

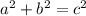
Where a and b are the legs and c is the hypotenuse.

1. Define Sides

The legs are the 2 shorter sides and the hypotenuse is the longest.

The sides given are 3, 4 (shorter), and 5 (longest). Therefore:

`a=3 \\b=4 \\c=5`

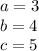
2. Check the Sides in the Theorem

Substitute the values into the theorem.

`(3)^2+(4)^2=(5)^2`

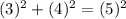
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Addition, and Subtraction.

Solve all of the exponents first.

• (3)² = 3*3= 9

• (4)²= 4*4= 16

`9+16=(5)^2`

• (5)²= 5*5= 25

`9+16=25`

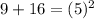
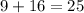
Add the numbers on the left side of the equation.

`25=25`

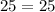
This is true. 25 is equal to 25, so this triangle can be a right triangle.