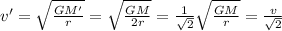Answer:
Step-by-step explanation:
To solve the problem, we can equate the gravitational force that keeps the satellite in orbit with the centripetal force:
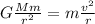
where
G is the gravitational constant
M is the mass of the planet
m is the mass of the satellite
v is the orbital speed of the satellite
r is the distance of the satellite from the planet's centre
Solving the formula for v,
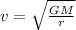
If the planet has half of the initial mass:
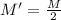 , the new orbital speed of the satellite will be
, the new orbital speed of the satellite will be