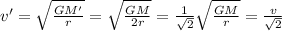Question

A satellite travels at orbital speed V around a planet of mass M. If the planet had half as much mass, what would be the new orbital speed of the satellite?

V/2

V

V

V/2

2V

Answer 1

`(v)/(√(2))`

Step-by-step explanation:

To solve the problem, we can equate the gravitational force that keeps the satellite in orbit with the centripetal force:

`G(Mm)/(r^2)=m(v^2)/(r)`

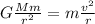
where

G is the gravitational constant

M is the mass of the planet

m is the mass of the satellite

v is the orbital speed of the satellite

r is the distance of the satellite from the planet's centre

Solving the formula for v,

`v=\sqrt{(GM)/(r)}`

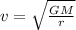
If the planet has half of the initial mass:
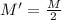`M' = (M)/(2)`, the new orbital speed of the satellite will be

`v'=\sqrt{(GM')/(r)}=\sqrt{(GM)/(2r)}=(1)/(√(2))\sqrt{(GM)/(r)}=(v)/(√(2))`