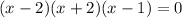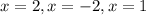ANSWER
The roots are -2,1 and 2
Step-by-step explanation
The given polynomial function is
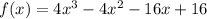
It was given that, (x-2) is a factor of the polynomial.
From the Remainnder Theorem this implies that f(2)=0.
We can rewrite the given polynomial as;
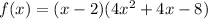
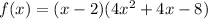
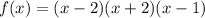
Hence the other roots are: