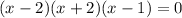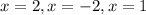Question

One factor it f(x) = 4x3 - 4x2 - 16x + 16 is (x -2). What are all the roots of the function? Use the remainder theorem

Answer 1

ANSWER

The roots are -2,1 and 2

Step-by-step explanation

The given polynomial function is


`f(x) = 4 {x}^(3) - 4 {x}^(2) - 16x + 16`

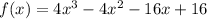
It was given that, (x-2) is a factor of the polynomial.

From the Remainnder Theorem this implies that f(2)=0.

We can rewrite the given polynomial as;


`f(x) = (x - 2)(4 {x}^(2) + 4x - 8)`


`f(x) = (x - 2)(4 {x}^(2) + 4x - 8)`


`f(x) = (x - 2)(x + 2)(x - 1)`

Hence the other roots are:


`(x - 2)(x + 2)(x - 1) = 0`


`x=2,x=-2,x=1`