Question

If a buffer contains 1.05M B and 0.750M BH+ has the pH of 9.5. What would be the pH after 0.005mol of HCL is added to 0.5L of solution

Answer 1

Calculate the new pH of a buffer solution after HCl is added by using the Henderson-Hasselbalch equation and adjusting the concentrations of the buffer components.

Step-by-step explanation:

The question involves calculating the pH of a buffer solution after the addition of HCl. In a buffer system containing 1.05M of B (a base) and 0.750M of BH+ (its conjugate acid), the pH is initially 9.5. To find the new pH after the addition of 0.005 mol of HCl to 0.5L of this buffer, we use the Henderson-Hasselbalch equation. Assuming that the volumes of the buffer and the added HCl are additive (which is a common approximation in buffer problems), we calculate the moles of HCl added and then adjust the concentration of BH+ and B accordingly, since HCl will convert B to BH+. With the new concentrations, we plug the values back into the Henderson-Hasselbalch equation to find the final pH.

Note: Without the specific pKa value or formula of the buffering agents, a numerical solution cannot be provided

Answer 2

Final pH: 9.49.

Round to two decimal places as in the question: 9.5.

Step-by-step explanation:

The conjugate of B is a cation that contains one more proton than B. The conjugate of B is an acid. As a result, B is a weak base.

What's the pKb of base B?

Consider the Henderson-Hasselbalch equation for buffers of a weak base and its conjugate acid ion.

`\displaystyle \text{pOH} = \text{pK}_b + \log{\frac{[\text{Salt}]}{[\text{Base}]}}`.

`\text{pOH} = \text{pK}_w - \text{pH}`.

`\text{pK}_w = 14`.

`\text{pOH} = 14 - 9.5 = 4.5`

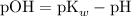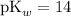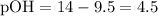
`\displaystyle \text{pK}_b = \text{pOH} -\log{\frac{[\text{Salt}]}{[\text{Base}]}}\\\phantom{\text{pK}_b} = 4.5 - \log{(0.750)/(1.05)} \\\phantom{\text{pK}_b} =4.64613`.

What's the new salt-to-base ratio?

The 0.005 mol of HCl will convert 0.005 mol of base B to its conjugate acid ion BH⁺.

Initial:

• 
  `n(\text{B}) = c\cdot V = 1.05 * 0.5 = 0.525\;\text{mol}`;
• 
  `n(\text{BH}^(+)) = c\cdot V = 0.750 * 0.5 = 0.375\;\text{mol}`.

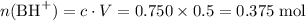After adding the HCl:

• 
  `n(\text{B}) = 0.525 - 0.005 = 0.520\;\text{mol}`;
• 
  `n(\text{BH}^(+)) = 0.375+ 0.005 = 0.380\;\text{mol}`.

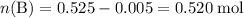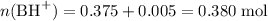Assume that the volume is still 0.5 L:

• 
  `\displaystyle [\text{B}] = (n)/(V) = (0.520)/(0.5) = 1.04\;\text{mol}\cdot\text{dm}^(-3)`.
• 
  `\displaystyle [\text{BH}^(+)] = (n)/(V) = (0.380)/(0.5) = 0.760\;\text{mol}\cdot\text{dm}^(-3)`.

What's will be the pH of the solution?

Apply the Henderson-Hasselbalch equation again:

`\displaystyle \text{pOH} = \text{pK}_b + \log{\frac{[\text{Salt}]}{[\text{Base}]}} = 4.64613 + \log{(0.760)/(1.04)} = 4.50991`

`\text{pH} = \text{pK}_w - \text{pOH}= 14 - 4.50991 = 9.49`.

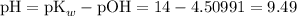The final pH is slightly smaller than the initial pH. That's expected due to the hydrochloric acid. However, the change is small due to the nature of buffer solutions: adding a small amount of acid or base won't significantly impact the pH of the solution.