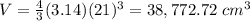Answer:
The volume of the container is
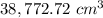
Explanation:
step 1
Find the radius of the sphere
we know that
The surface area of a sphere is equal to
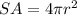
we have
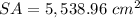
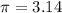
substitute the values and solve for r
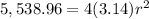
![r^(2)=5,538.96/[4(3.14)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mfdtzz078e5qznotysb63myv75h9scrhgm.png)
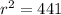
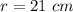
step 2
Find the volume of the container
The volume of the sphere (container) is equal to

we have
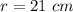
substitute the values