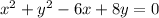Question

Write the general equation for the circle that passes through the points:

(0, 0)
(6, 0)
(0, - 8)
You must include the appropriate sign (+ or -) in your answer. Do not use spaces in your answer.
x^2 + y^2 ____ x ____ y = 0

Please Help!

Answer 1

`x^(2) + y^(2) -6x+8y= 0`

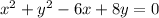
Explanation:

The general equation of the circle is of the form:

`x^(2) + y^(2) +2gx+2fy + c= 0`

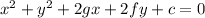
The circle passes through the point (0,0), this means replacing x = 0 and y = 0 must satisfy the equation Using these values, we get:

`0^(2) +0^(2)+2g(0)+2f(0)+c=0\\c=0`

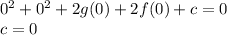
This means value of c is zero for the given circle. So, now the equation of the circle is:

`x^(2) + y^(2) +2gx+2fy= 0`

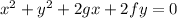
Now using the point, (6, 0) in this equation, we get:

`6^(2)+ 0^(2)+2g(6)+2f(0)=0\\36+12g=0\\36=-12g\\g=-3`

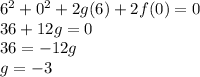
Hence the value of g is -3, using the value of g and c in our equation, the equation becomes:

`x^(2) + y^(2) -6x+2fy= 0`

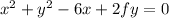
Now using the 3rd point (0, -8) in this equation to find the value of f:

`0^(2)+ (-8)^(2)-6(0)+2f(-8)=0\\64-16f=0\\64=16f\\f=4`

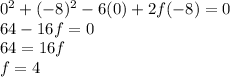
Using the value of g, f and c, the final equation of the circle is:

`x^(2) + y^(2) -6x+8y= 0`