Question

Determine which polynomial is a perfect square trinomial.

25x2 − 40x − 16

9a2 − 20a − 25

25b2 − 15b + 9

16x2 − 56x + 49

Answer 1

D.

16x2-56x+49 is correct!

Explanation:

Answer 2

16x² − 56x + 49

Explanation:

The square of difference of two terms can be expressed as a perfect square trinomial in the following manner:

`(a-b)^(2)=a^(2)-2ab+b^(2)`

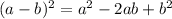
The symbol with square terms must be always positive. So this removes the first two options from the given choices. The correct option is either c or d.

Only the option d can be expressed as a perfect square as shown below:

`16x^(2)-56x+49\\\\ = (4x)^(2)-2(4x)(7)+(7)^(2)\\\\ =(4x - 7)^(2)`

Option c would have been correct if it was -30b instead of -15b i.e. the middle term is twice the product of first and second term.

So, option D is correct