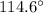Question

Find the measure of CD

Answer 1

The measure of arc CD is
`114.6\°`

Explanation:

see the attached figure with letters to better understand the problem

we know that

The measure of arc CD is equal to the angle CAD by central angle

The measure of angle CAD is equal to the angle CAB multiplied by 2

Find the measure of angle CAB

In the right triangle ABC

`sin(CAB)=(BC)/(AC)`

`BC=BD=36.7/2=18.35\ in`

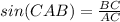
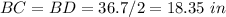
substitute the values

`sin(CAB)=(18.35)/(21.8)`

`< CAB=arcsin((18.35)/(21.8))=57.32\°`

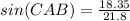
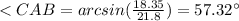
Find the measure of angle CAD

`m<CAD=2*m<CAB`

`m<CAD=2*(57.32\°)=114.6\°`

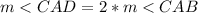
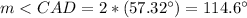
therefore

The measure of arc CD is
`114.6\°`