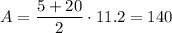Question

Given: ABCD is a trapezoid, AB = 13,CD = 14, BC = 5, and AD = 20. Find: AABCD

Answer 1

A=140sq. units

Explanation:

sorry, but i don't really know how to do it. :(

Answer 2

140

Explanation:

Consider trapezoid ABCD. Draw two heights BE and CF. Quadrilateral BEFC is a rectangle, then EF = BC = 5 and BE = CF = y.

Let AE = x, then FD = AD - AE - EF = 20 - x - 5 = 15 - x.

Triangles ABE and CDF are two right triangles. By the Pythagorean theorem,

`AB^2=BE^2 +AE^2,\\ \\CD^2=CF^2+DF^2.`

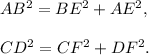
Thus,

`13^2=y^2+x^2,\\ \\14^2=(15-x)^2+y^2.`

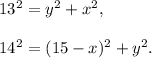
Subtract from the second equation the first one:

`14^2-13^2=(15-x)^2-x^2,\\ \\196-169=225-30x+x^2-x^2,\\ \\30x=225-196+169,\\ \\30x=198,\\ \\x=6.6.`

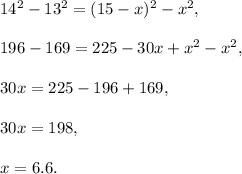
Therefore,

`169=6.6^2+y^2,\\ \\y^2=169-43.56,\\ \\y^2=125.44,\\ \\y=11.2.`

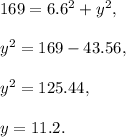
The area of the trapezoid is

`A=(5+20)/(2)\cdot 11.2=140`