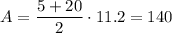Answer:
140
Explanation:
Consider trapezoid ABCD. Draw two heights BE and CF. Quadrilateral BEFC is a rectangle, then EF = BC = 5 and BE = CF = y.
Let AE = x, then FD = AD - AE - EF = 20 - x - 5 = 15 - x.
Triangles ABE and CDF are two right triangles. By the Pythagorean theorem,
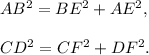
Thus,
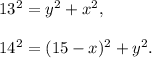
Subtract from the second equation the first one:
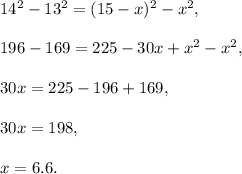
Therefore,
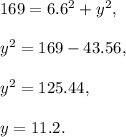
The area of the trapezoid is