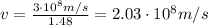Question

The wavelength of red helium-neon laser light in air is 632.8 nm.

(a) What is its frequency?
(b) What is its wavelength in glass that has an index of refractionof 1.48?
(c) What is its speed in the glass?

Answer 1

(a)
`4.74\cdot 10^14 Hz`

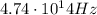
The frequency of an electromagnetic wave is given by:

`f=(c)/(\lambda)`

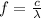
where

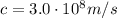`c=3.0\cdot 10^8 m/s` is the speed of the wave in a vacuum (speed of light)

`\lambda` is the wavelength

In this problem, we have laser light with wavelength

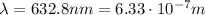`\lambda=632.8 nm=6.33\cdot 10^(-7) m`. Substituting into the formula, we find its frequency:

`f=(3.0\cdot 10^8 m/s)/(6.33\cdot 10^(-7) m)=4.74\cdot 10^14 Hz`

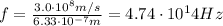
(b) 427.6 nm

The wavelength of an electromagnetic wave in a medium is given by:

`\lambda=(\lambda_0)/(n)`

where

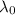`\lambda_0` is the original wavelength in a vacuum (approximately equal to that in air)

`n` is the index of refraction of the medium

In this problem, we have

`\lambda_0=632.8 nm`

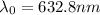
n = 1.48 (index of refraction of glass)

Substituting into the formula,

`\lambda=(632.8 nm)/(1.48)=427.6 nm`

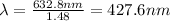
(c)
`2.03\cdot 10^8 m/s`

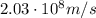
The speed of an electromagnetic wave in a medium is

`v=(c)/(n)`

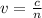
where c is the speed of light in a vacuum and n is the refractive index of the medium.

Since in this problem n=1.48, we find

`v=(3\cdot 10^8 m/s)/(1.48)=2.03\cdot 10^8 m/s`