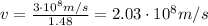(a)
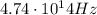
The frequency of an electromagnetic wave is given by:
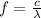
where
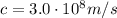 is the speed of the wave in a vacuum (speed of light)
is the speed of the wave in a vacuum (speed of light)
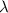 is the wavelength
is the wavelength
In this problem, we have laser light with wavelength
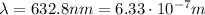 . Substituting into the formula, we find its frequency:
. Substituting into the formula, we find its frequency:
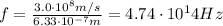
(b) 427.6 nm
The wavelength of an electromagnetic wave in a medium is given by:
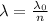
where
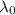 is the original wavelength in a vacuum (approximately equal to that in air)
is the original wavelength in a vacuum (approximately equal to that in air)
 is the index of refraction of the medium
is the index of refraction of the medium
In this problem, we have
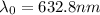
n = 1.48 (index of refraction of glass)
Substituting into the formula,
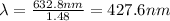
(c)
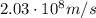
The speed of an electromagnetic wave in a medium is
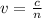
where c is the speed of light in a vacuum and n is the refractive index of the medium.
Since in this problem n=1.48, we find