Answer: Choice C)

====================================
Work Shown:
Part 1
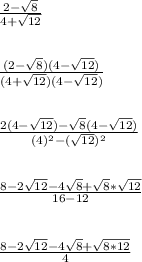
Part 2
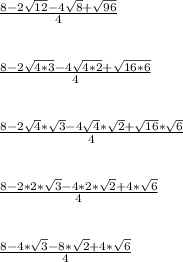
Part 3
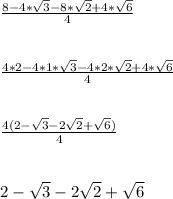
This shows the answer is choice C.
----------------------------------------------
Step-by-step explanation:
There are a lot of steps, so I broke things up into 3 sections or parts. The idea I'm applying is if the denominator is of the form
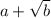 , then multiplying top and bottom by
, then multiplying top and bottom by
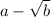 will rationalize the denominator. This is due to the difference of squares rule (step 3 of part 1). The following step shows squaring a square root has the two cancel out.
will rationalize the denominator. This is due to the difference of squares rule (step 3 of part 1). The following step shows squaring a square root has the two cancel out.
From that point, I simplified each square root and factored to cancel out a pair of '4's.
To expand out
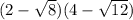 , we can use either the FOIL method, the box method, or the distribution property. I used the distribution property.
, we can use either the FOIL method, the box method, or the distribution property. I used the distribution property.