Which number line shows the solution set for |d| > 3?

Question

asked May 22, 2020 134k views

2 Answers

Atavio · Answer 1 · 2020-05-23T07:30:38+0000

Answer:

Last option

d>3 or
d<-3

Explanation:

The absolute value is a function that transforms any value x into a positive number.

Therefore, for the function
f(x) = |x| x> 0 for all real numbers.

Then the inequation:

|d|> 3 has two cases

(d) if
d>0 (i)

-(d) if
d< 0 (ii)

We solve the case (i)

d> 3

We solve the case (ii)

$-d>3\\d < -3$

Then the solution is:

d>3 or
d<-3

UrOutsourced · Answer 2 · 2020-05-28T18:07:29+0000

Answer:

Last choice is the correct graph.

Explanation:

We have been given inequality
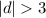|d|>3 . Now we need to find out which of the given number lines shows the correct solution set for
|d|>3 .

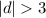We know that
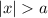|x|>a can be broken into :

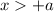x>+a or
x<-a

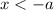
Same way we can break
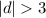|d|>3 into two parts as:

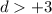d>+3 or
d<-3

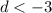
Since it has only < symbol but not equal so we make an open circle at both +3 and -3.

Hence last choice is the correct graph.