Question 1:
For this case we must find the derivative of the following function:
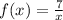 evaluated at
evaluated at
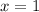
We have by definition:
![\frac {d} {dx} [x ^ n] = nx ^ {n-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7cskpzxcborerutaq9r6teqb4uv61uk0wt.png)
So:
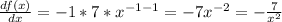
We evaluate in
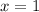
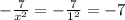
ANswer:
Option A
Question 2:
For this we must find the derivative of the following function:
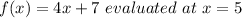
We have by definition:
![\frac {d} {dx} [x ^ n] = nx ^ {n-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7cskpzxcborerutaq9r6teqb4uv61uk0wt.png)
The derivative of a constant is 0
So:
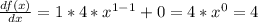
Thus, the value of the derivative is 4.
Answer:
Option A
Question 3:
For this we must find the derivative of the following function:
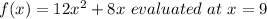
We have by definition:
![\frac {d} {dx} [x ^ n] = nx ^ {n-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7cskpzxcborerutaq9r6teqb4uv61uk0wt.png)
So:
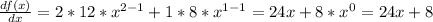
We evaluate for
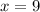 we have:
we have:
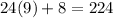
Answer:
Option D
Question 4:
For this we must find the derivative of the following function:
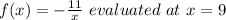
We have by definition:
![\frac {d} {dx} [x ^ n] = nx ^ {n-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7cskpzxcborerutaq9r6teqb4uv61uk0wt.png)
So:
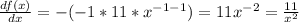
We evaluate for
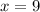 and we have:
and we have:
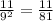
ANswer:
Option D
Question 5:
For this case we have by definition, that the derivative of the position is the velocity. That is to say:
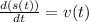
Where:
s: It's the position
v: It's the velocity
t: It's time
We have the position is:
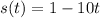
We derive:
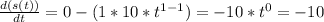
So, the instantaneous velocity is -10
Answer:
-10