Question

Question 1(Multiple Choice Worth 2 points) Find the derivative of f(x) = 7 divided by x at x = 1.

-7
-1
1
7
Question 2(Multiple Choice Worth 2 points) Find the derivative of f(x) = 4x + 7 at x = 5.
4
1
5
7
Question 3(Multiple Choice Worth 2 points) Find the derivative of f(x) = 12x2 + 8x at x = 9.
256
-243
288
224
Question 4(Multiple Choice Worth 2 points) Find the derivative of f(x) = negative 11 divided by x at x = 9.
11/9
81/11
9/11
11/81
Question 5 (Essay Worth 2 points) The position of an object at time t is given by s(t) = 1 - 10t. Find the instantaneous velocity at t = 10 by finding the derivative.

Answer 1

Explanation:

Answer 2

Question 1:

For this case we must find the derivative of the following function:

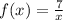`f (x) = \frac {7} {x}` evaluated at
`x = 1`

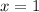
We have by definition:

`\frac {d} {dx} [x ^ n] = nx ^ {n-1}`

So:

`\frac {df (x)} {dx} = - 1 * 7 * x ^ {- 1-1} = - 7x ^ {- 2} = - \frac {7} {x ^ 2}`

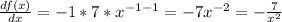
We evaluate in
`x = 1`

`- \frac {7} {x ^ 2} = - \frac {7} {1 ^ 2} = - 7`

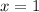
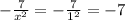
ANswer:

Option A

Question 2:

For this we must find the derivative of the following function:

`f (x) = 4x + 7\ evaluated\ at\ x = 5`

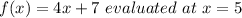
We have by definition:

`\frac {d} {dx} [x ^ n] = nx ^ {n-1}`

The derivative of a constant is 0

So:

`\frac {df (x)} {dx} = 1 * 4 * x ^ {1-1} + 0 = 4 * x ^ 0 = 4`

Thus, the value of the derivative is 4.

Answer:

Option A

Question 3:

For this we must find the derivative of the following function:

`f (x) = 12x ^ 2 + 8x\ evaluated\ at\ x = 9`

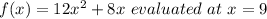
We have by definition:

`\frac {d} {dx} [x ^ n] = nx ^ {n-1}`

So:

`\frac {df (x)} {dx} = 2 * 12 * x ^ {2-1} + 1 * 8 * x ^ {1-1} = 24x + 8 * x ^ 0 = 24x + 8`

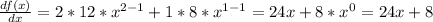
We evaluate for
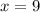`x = 9`we have:

`24 (9) + 8 = 224`

Answer:

Option D

Question 4:

For this we must find the derivative of the following function:

`f (x) = - \frac {11} {x}\ evaluated\ at\ x = 9`

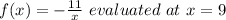
We have by definition:

`\frac {d} {dx} [x ^ n] = nx ^ {n-1}`

So:

`\frac {df (x)} {dx} = - (- 1 * 11 * x ^ {- 1-1}) = 11x ^ {- 2} = \frac {11} {x ^ 2}`

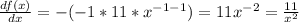
We evaluate for
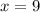`x = 9` and we have:

`\frac {11} {9 ^ 2} = \frac {11} {81}`

ANswer:

Option D

Question 5:

For this case we have by definition, that the derivative of the position is the velocity. That is to say:

`\frac {d (s (t))} {dt} = v (t)`

Where:

s: It's the position

v: It's the velocity

t: It's time

We have the position is:

`s (t) = 1-10t`

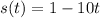
We derive:

`\frac {d (s (t))} {dt} = 0- (1 * 10 * t ^ {1-1}) = - 10 * t ^ 0 = -10`

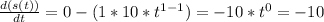
So, the instantaneous velocity is -10

Answer:

-10