Question

Given: m

EL
=(2x)°, m
LG
=(3x)°
m
GF
=(4x−8)°, m
FE
=(x−12)°
Find: m∠LTE

Answer 1

m∠LTE = 110°

Explanation:

We know that sum of all arcs of a circle is 360°

Therefore
`m(arcAL)+m(arcLG)+m(arcGF)+(mFE)=360`

Now we put the values of each arc

`(2x)+(3x)+(4x-8)+(x-12)=2x+3x+4x+x-8-12=10x-20=360`

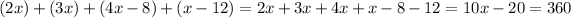
10x = 360 + 20

10x = 380

`x=(380)/(10)`

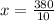
x = 38

Now from the theorem of intersecting chords in a circle

Measure of ∠LTE =
`(1)/(2)[m(arcEL)+m(arcGF)]`

m(arc EL) = 2x = 2×38 = 76°

m(arc GF) = (4x - 8) = (4×38 - 8) = (152 - 8) = 144°

Now we can get the measure of ∠LTE

m∠LTE =
`(1)/(2)(76 + 144)=(220)/(2)=110`

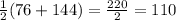
Therefore m∠LTE = 110° is the answer.

Answer 2

m∠LTE = 110

Explanation:

1. add up all of the arcs.

2x+3x+4x-8+x-12

2. all of the arcs equal 360

2x+3x+4x-8+x-12=360

3. Find x

10x-20=360, x=38

4. angle LTE is equal to half of the sum of the intercepted arcs.

0.5(arc LE +GF)

5. plug in LE +GF with x

.5(76+144)