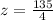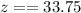Answer:

Explanation:
We are given that z varies inversely with x and directly with y when x=6 and y=2 then z=5
We have to find the value of z when x=4 and y=9
According to question
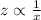
and

Therefore, we have
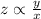
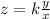
k=proportionality constant
Substitute x=6 , y=2 and z=5 then we get
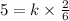
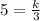
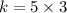
By division poperty of equality
k=15
Now, substitute the value x=4,y=9 and k=15 then the value of z