Question

Determine the graph of the polar equation r =6/2-2cos theta.

Answer 1

D

Explanation:

edge

Answer 2

Choice D is correct

Explanation:

The first step is to write the polar equation of the conic section in standard form by dividing both the numerator and the denominator by 2;

`r=(3)/(1-cos(theta))`

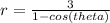
The eccentricity of this conic section is thus 1, the coefficient of cos θ. Thus, this conic section is a parabola since its eccentricity is 1.

The value of the directrix is determined as;

d = k/e = 3/1 = 3

The denominator of the polar equation of this conic section contains (-cos θ) which implies that this parabola opens towards the right and thus the equation of its directrix is;

x = -3

Thus, the polar equation represents a parabola that opens towards the right with a directrix located at x = -3. Choice D fits this criteria