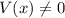Answer:
Third option
x ≠2 and x cannot be any value for which v(x) = 0
Explanation:
In this problem we are asked to find the domain of the function
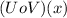
We know that
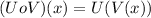 .
.
We know that:
Domain of U(x) is all real numbers except x = 0
Domain of V(x) is all real numbers except x = 2.
Then the domain of the composite function U(V (x)) is:
all real numbers except x = 2. (since x = 2 does not belong to the domain of V(x) and all values of x for which V(x) = 0 (since x = 0 does not belong to the domain of U(x))
Finally the domain of
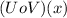 ) is:
) is:
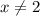 and
and