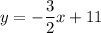Answer:
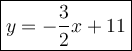
Explanation:
The slope-intercept form of an equation of a line:

m - slope
b - y-intercept
The formula of a slope:
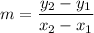
We have the point A(8, -1) and B(-4, 17). Substitute:
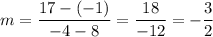
The equation of a line:
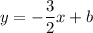
Put the coordinates of the point A(8, -1) to the equation of a line:
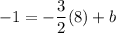
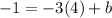
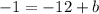 add 12 to both sides
add 12 to both sides
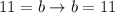
Finally we have the equation of a line in a slope-intercept form: