Question

Please explain how to solve it​

Answer 1

Answer:
`(8x^3)/(27y^6)`

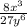
This is the fraction 8x^3 all over 27y^6

On a keyboard, we can write it as (8x^3)/(27y^6)

===========================================================

Step-by-step explanation:

The exponent tells you how many copies of the base to multiply with itself.

We'll have three copies of
`\left((2x)/(3y^2)\right)` multiplied with itself due to the cube exponent on the outside.

So,

`\left((2x)/(3y^2)\right)^3 = \left((2x)/(3y^2)\right)*\left((2x)/(3y^2)\right)*\left((2x)/(3y^2)\right)\\\\\left((2x)/(3y^2)\right)^3 = (2x*2x*2x)/((3y^2)*(3y^2)*(3y^2))\\\\\left((2x)/(3y^2)\right)^3 = ((2*2*2)*(x*x*x))/((3*3*3)*(y^2*y^2*y^2))\\\\\left((2x)/(3y^2)\right)^3 = (8x^3)/(9y^6)\\\\`

-------------------

Or another approach you could take is to cube each component of the fraction. The rule I'm referring to is
`\left((a)/(b)\right)^c = (a^c)/(b^c)`

Applying that rule will lead to:

`\left((2x)/(3y^2)\right)^3 = ((2x)^3)/((3y^2)^3)\\\\\left((2x)/(3y^2)\right)^3 = (2^3*x^3)/(3^3*(y^2)^3)\\\\\left((2x)/(3y^2)\right)^3 = (8x^3)/(27y^(2*3))\\\\\left((2x)/(3y^2)\right)^3 = (8x^3)/(27y^6)\\\\`

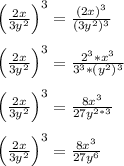
Either way you should get 8x^3 all over 27y^6 as one fraction.

Answer 2

You just distribute the power of 3 so it should end up as
(8x^3)/(27y^6)

(the 3 and the 2 multiply to equal 6)

Hope it helps!