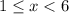What is the solution to the compound inequality 3x − 8 ≥ −5 and 2x − 7 < 5? x ≤ 1 and x > 6 1 ≤ x < 6 x > 1 and x > 6 1 < x < 6

Question

asked Mar 9, 2020 102k views

2 Answers

Thenewbie · Answer 1 · 2020-03-16T20:46:30+0000

The solution to the compound inequality is given by:

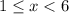
$1\leq x<6$

The compound inequality is given by:

$3x-8\geq -5$ and

2x-7<5

$3x-8\geq -5$

on adding both side of the inequality by 8 we get:

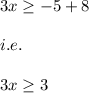
$3x\geq -5+8\\\\i.e.\\\\3x\geq 3$

Now on dividing both side of the inequality by 3 we get:

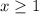
$x\geq 1$

2x-7<5

On adding both side of the inequality by 7 we get:

$2x<5+7\\\\i.e.\\\\2x<12$

on dividing both side of the inequality by 2 we get:

x<6

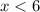
Hence, the solution of the compound inequality is:

$1\leq x<6$