Answer: The side length of the inner square is 17.3 ft.
Step-by-step explanation: Given that a community is building a square garden with a walkway around the perimeter with the design shown at the right.
We are to find the area of the inner square equal to 75% of the total area of the garden.
The step-wise solutions area s follows:
(1) From the figure, we note that
The side length of the inner square is x ft.
We know that the area of a square is equal to (side)².
So, the area of the inner square will be
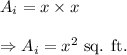
(2) The whole garden is in the form of a square with side length 20 ft.
Therefore, the area of the entire garden is given by
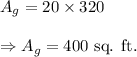
(3) The area of the entire garden is 400 sq. ft.
So, 75% of the area of the entire garden will be
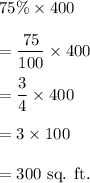
(4) Since the area of the inner square is equal to 75% of the area of the entire garden, so we must have
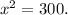
(5) The solution of the quadratic equation is as follows:
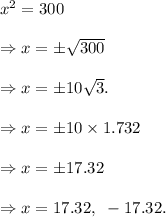
So, the required solution is x = 17.32, - 17.32.
Rounding to nearest tenth, we get
x=17.3, - 17.3.
(6) Since the length of the side of a square cannot be negative, so the solution that best describes the side length of the inner square will be
x = 17.3.
Thus, all the questions are answered.
And, the side length of the inner square is 17.3 ft.