Question

A community is building a square garden with a walkway around the perimeter with the design shown at the right. Find the side length of the inner square that would make the area of the inner square equal to 75% of the total area of the garden. Round to the nearest tenth of a foot.

1. What is an expression for the area of the inner square?



2. What is the area of the entire garden?



3. What is 75% of the area of the entire garden?



4. Write an equation for the area of the inner square using the expressions from Steps 1 and 3.



5. Solve the quadratic equation. Round to the nearest tenth of a foot.



6. Which solution to the quadratic equation best describes the side length of the inner square? Explain.

Answer 1

1. idk
2. 20×20=400 square feet
3. 0.75×400=300 square feet
4. (20×20)×0.75
5. idk
6. idk

Answer 2

Answer: The side length of the inner square is 17.3 ft.

Step-by-step explanation: Given that a community is building a square garden with a walkway around the perimeter with the design shown at the right.

We are to find the area of the inner square equal to 75% of the total area of the garden.

The step-wise solutions area s follows:

(1) From the figure, we note that

The side length of the inner square is x ft.

We know that the area of a square is equal to (side)².

So, the area of the inner square will be

`A_i=x* x\\\\\Rightarrow A_i=x^2~\textup{sq. ft}.`

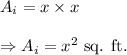
(2) The whole garden is in the form of a square with side length 20 ft.

Therefore, the area of the entire garden is given by

`A_g=20* 320\\\\\Rightarrow A_g=400~\textup{sq. ft}.`

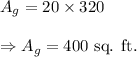
(3) The area of the entire garden is 400 sq. ft.

So, 75% of the area of the entire garden will be

`75\%* 400\\\\=(75)/(100)* 400\\\\=(3)/(4)* 400\\\\=3* 100\\\\=300~\textup{sq. ft}.`

(4) Since the area of the inner square is equal to 75% of the area of the entire garden, so we must have

`x^2=300.`

(5) The solution of the quadratic equation is as follows:

`x^2=300\\\\\Rightarrow x=\pm√(300)\\\\\Rightarrow x=\pm10√(3).\\\\\Rightarrow x=\pm10* 1.732\\\\\Rightarrow x=\pm17.32\\\\\Rightarrow x=17.32,~-17.32.`

So, the required solution is x = 17.32, - 17.32.

Rounding to nearest tenth, we get

x=17.3, - 17.3.

(6) Since the length of the side of a square cannot be negative, so the solution that best describes the side length of the inner square will be

x = 17.3.

Thus, all the questions are answered.

And, the side length of the inner square is 17.3 ft.