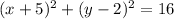Question

A diameter of a circle had endpoints of (-5, 6) and (-5,-2). What is the equation of this circle?

Answer 1

Answer: OPTION A

Explanation:

Apply the formula for calculate the distance between two points to know the value of the diameter of the circle:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)\\D=√((-5-(-5))^2+(-2-6)^2)\\D=8`

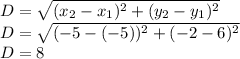
The equation of the circle is standard form is:

`(x-h)^2+(y-k)^2=r^2`

Where r is the radius and (h,k) is the point of the center of the circle.

As we know the diameter, we can find the radius:

`r=(8)/(2)=4`

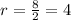
Substitute it into the equation:

`(x-h)^2+(y-k)^2=(4)^2`

`(x-h)^2+(y-k)^2=16`

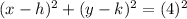
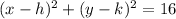
Then, the answer is:

`(x+5)^2+(y-2)^2=16`