The robot has acceleration vector
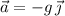
where
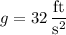 is the acceleration due to gravity.
is the acceleration due to gravity.
Its initial velocity is
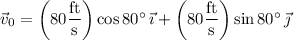
so that its velocity at time
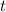 is
is
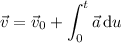
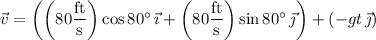
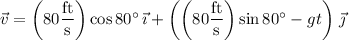
If we take the robot's starting position to be the origin, so that
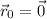 , then its position vector at time
, then its position vector at time
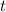 is
is
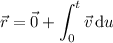
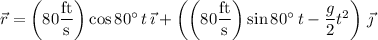
The rocket is 10 feet horizontally away from its starting point when
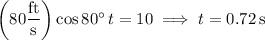
At this point, its vertical position is
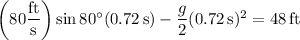
above the ground.