Answer:
option C
12
Explanation:
Given in the question an expression
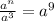
To solve for n we will use rules of exponent
cross multiply
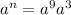
apply product rule
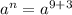
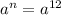
Apply logarithm on both sides of equation
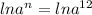
apply power rule of logarithm
nln(a) = 12ln(a)
ln(a) will cancel out on each side so we are left with
n= 12