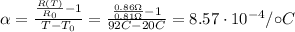Question

A 1.20-m cylindrical rod of diameter 0.570 cm is connected to a power supply that maintains a constant potential difference of 15.0 V across its ends, while an ammeter measures the current through it. You observe that at room temperature (20.0°C) the ammeter reads 18.6 A, while at 92.0°C it reads 17.5 A. You can ignore any thermal expansion of the rod. (a) Find the resistivity at 20°C for the material of the rod. (b) Find the temperature coefficient of resistivity at 20°C for the material of the rod.

Answer 1

(a)
`1.72\cdot 10^(-5) \Omega m`

The resistance of the rod is given by:

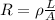`R=\rho (L)/(A)` (1)

where

`\rho` is the material resistivity

L = 1.20 m is the length of the rod

A is the cross-sectional area

The radius of the rod is half the diameter:
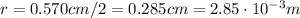`r=0.570 cm/2=0.285 cm=2.85\cdot 10^(-3) m`, so the cross-sectional area is

`A=\pi r^2=\pi (2.85\cdot 10^(-3) m)^2=2.55\cdot 10^(-5) m^2`

The resistance at 20°C can be found by using Ohm's law. In fact, we know:

- The voltage at this temperature is V = 15.0 V

- The current at this temperature is I = 18.6 A

So, the resistance is

`R=(V)/(I)=(15.0 V)/(18.6 A)=0.81 \Omega`

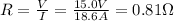
And now we can re-arrange the eq.(1) to solve for the resistivity:

`\rho=(RA)/(L)=((0.81 \Omega)(2.55\cdot 10^(-5) m^2))/(1.20 m)=1.72\cdot 10^(-5) \Omega m`

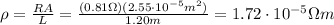
(b)
`8.57\cdot 10^(-4) /{\circ}C`

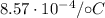
First of all, let's find the new resistance of the wire at 92.0°C. In this case, the current is

I = 17.5 A

So the resistance is

`R=(V)/(I)=(15.0 V)/(17.5 A)=0.86 \Omega`

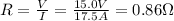
The equation that gives the change in resistance as a function of the temperature is

`R(T)=R_0 (1+\alpha(T-T_0))`

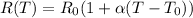
where

`R(T)=0.86 \Omega` is the resistance at the new temperature (92.0°C)

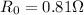`R_0=0.81 \Omega` is the resistance at the original temperature (20.0°C)

`\alpha` is the temperature coefficient of resistivity

`T=92^(\circ)C`

`T_0 = 20^(\circ)`

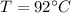
Solving the formula for
`\alpha`, we find

`\alpha=((R(T))/(R_0)-1)/(T-T_0)=((0.86 \Omega)/(0.81 \Omega)-1)/(92C-20C)=8.57\cdot 10^(-4) /{\circ}C`