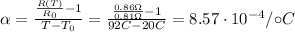(a)
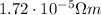
The resistance of the rod is given by:
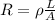 (1)
(1)
where
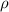 is the material resistivity
is the material resistivity
L = 1.20 m is the length of the rod
A is the cross-sectional area
The radius of the rod is half the diameter:
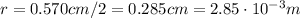 , so the cross-sectional area is
, so the cross-sectional area is
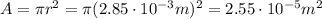
The resistance at 20°C can be found by using Ohm's law. In fact, we know:
- The voltage at this temperature is V = 15.0 V
- The current at this temperature is I = 18.6 A
So, the resistance is
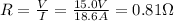
And now we can re-arrange the eq.(1) to solve for the resistivity:
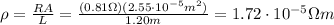
(b)
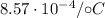
First of all, let's find the new resistance of the wire at 92.0°C. In this case, the current is
I = 17.5 A
So the resistance is
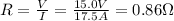
The equation that gives the change in resistance as a function of the temperature is
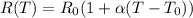
where
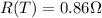 is the resistance at the new temperature (92.0°C)
is the resistance at the new temperature (92.0°C)
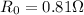 is the resistance at the original temperature (20.0°C)
is the resistance at the original temperature (20.0°C)
 is the temperature coefficient of resistivity
is the temperature coefficient of resistivity
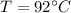
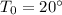
Solving the formula for
 , we find
, we find