Solve the linear equation ((16)/(9))^(-2x+5) = ((3)/(4))^(x-7)

Question

Solve the linear equation


`((16)/(9))^(-2x+5) = ((3)/(4))^(x-7)`

Answer 1

Graph both equations and find the X value when the lines cross.

See attached picture of the graph

X = 1

Or you could take logarithms of both sides where log(a^b) = b loga to also find the value of x.

Answer 2

x = 1

Explanation:

Given in the question,

`(16/9)^(-2x+5) = (3/4)^((x-7))`

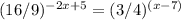
Take logarithm on both sides

`ln(16/9)^(-2x+5) = ln(3/4)^((x-7))`

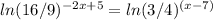
Apply power rule of logarithm

(-2x+5)ln(16/9) = (x-7)ln(3/4)

cross multiply

(-2x+5)/(x-7) =
`(ln(3/4))/(ln(16/9))`

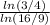
-1/2 = (-2x+5)/(x-7)

-(x-7) = 2(-2x+5)

-x + 7 = -4x + 10

rearrange the terms, x terms to left and constant to right

-x + 4x = 10 - 7

3x = 3

x = 1