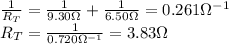Before starting with the problem, let's remind that:
- Total resistance of a combination of resistors in series is:
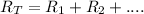
- Total resistance of a combination of resistors in parallel is given by:
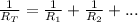
Now let's apply these equations to solve the different parts of the problem:
1. All the resistors in series:
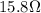
In this case, the total resistance is
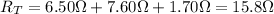
2. All the resistors are connected in parallel:
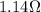
In this case, the total resistance is
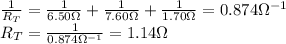
3. The 6.50 Ω and 7.60 Ω resistors are connected in parallel, and the 1.70-Ω resistor is connected in series with the parallel combination:
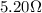
The total resistance of the two resistors connected in parallel is
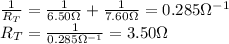
And the combination of these with the other resistor of 1.70-Ω in series gives a total resistance of
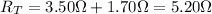
4. The 6.50 Ω and 1.70 Ω resistors are connected in parallel, and the 7.60-Ω resistor is connected in series with the parallel combination:
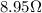
The total resistance of the two resistors connected in parallel is
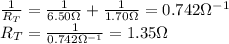
And the combination of these with the other resistor of 7.60-Ω in series gives a total resistance of
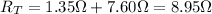
5. The 7.60 Ω and 1.70 Ω resistors are connected in parallel, and the 6.50-Ω resistor is connected in series with the parallel combination:
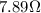
The total resistance of the two resistors connected in parallel is
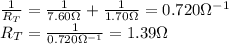
And the combination of these with the other resistor of 6.50-Ω in series gives a total resistance of
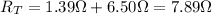
6. The 6.50 Ω and 7.60 Ω resistors are connected in series, and the 1.70-Ω resistor is connected in parallel with the series combination:
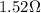
In this case, the total resistance of the two resistors in series is
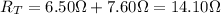
And the combination of these with the other resistor of 1.70-Ω in parallel gives a total resistance of
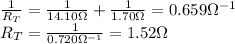
7. The 6.50 Ω and 1.70 Ω resistors are connected in series, and the 7.60-Ω resistor is connected in parallel with the series combination:
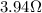
In this case, the total resistance of the two resistors in series is
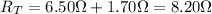
And the combination of these with the other resistor of 7.60-Ω in parallel gives a total resistance of
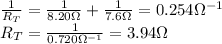
8. The 7.60 Ω and 1.70 Ω resistors are connected in series, and the 6.50-Ω resistor is connected in parallel with the series combination:
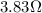
In this case, the total resistance of the two resistors in series is
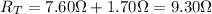
And the combination of these with the other resistor of 6.50-Ω in parallel gives a total resistance of