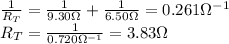Question

Eight different values of resistance can be obtained by connecting together three resistors 6.50 Ω, 7.60 Ω, and 1.70 Ω in all possible ways. What are the values in the following situations? All the resistors are connected in series. Ω All the resistors are connected in parallel. Ω The 6.50 Ω and 7.60 Ω resistors are connected in parallel, and the 1.70-Ω resistor is connected in series with the parallel combination. Ω The 6.50 Ω and 1.70 Ω resistors are connected in parallel, and the 7.60-Ω resistor is connected in series with the parallel combination. Ω The 7.60 Ω and 1.70 Ω resistors are connected in parallel, and the 6.50-Ω resistor is connected in series with the parallel combination. Ω The 6.50 Ω and 7.60 Ω resistors are connected in series, and the 1.70-Ω resistor is connected in parallel with the series combination. Ω The 6.50 Ω and 1.70 Ω resistors are connected in series, and the 7.60-Ω resistor is connected in parallel with the series combination. Ω The 7.60 Ω and 1.70 Ω resistors are connected in series, and the 6.50-Ω resistor is connected in parallel with the series combination. Ω Additional Materials

Answer 1

Before starting with the problem, let's remind that:

- Total resistance of a combination of resistors in series is:

`R_T=R_1+R_2+....`

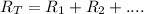
- Total resistance of a combination of resistors in parallel is given by:

`(1)/(R_T)=(1)/(R_1)+(1)/(R_2)+...`

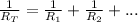
Now let's apply these equations to solve the different parts of the problem:

1. All the resistors in series:
`15.8 \Omega`

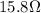
In this case, the total resistance is

`R_T=6.50\Omega +7.60\Omega+1.70\Omega=15.8 \Omega`

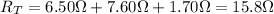
2. All the resistors are connected in parallel:
`1.14 \Omega`

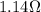
In this case, the total resistance is

`(1)/(R_T)=(1)/(6.50 \Omega)+(1)/(7.60 \Omega)+(1)/(1.70 \Omega)=0.874\Omega^(-1)\\R_T=(1)/(0.874 \Omega^(-1))=1.14 \Omega`

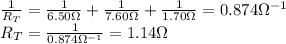
3. The 6.50 Ω and 7.60 Ω resistors are connected in parallel, and the 1.70-Ω resistor is connected in series with the parallel combination:
`5.20 \Omega`

The total resistance of the two resistors connected in parallel is

`(1)/(R_T)=(1)/(6.50 \Omega)+(1)/(7.60\Omega)=0.285\Omega^(-1)\\R_T=(1)/(0.285 \Omega^(-1))=3.50 \Omega`

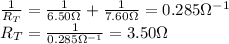
And the combination of these with the other resistor of 1.70-Ω in series gives a total resistance of

`R_T=3.50 \Omega+1.70 \Omega=5.20 \Omega`

4. The 6.50 Ω and 1.70 Ω resistors are connected in parallel, and the 7.60-Ω resistor is connected in series with the parallel combination:
`8.95 \Omega`

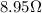
The total resistance of the two resistors connected in parallel is

`(1)/(R_T)=(1)/(6.50 \Omega)+(1)/(1.70\Omega)=0.742\Omega^(-1)\\R_T=(1)/(0.742 \Omega^(-1))=1.35 \Omega`

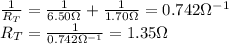
And the combination of these with the other resistor of 7.60-Ω in series gives a total resistance of

`R_T=1.35 \Omega+7.60 \Omega=8.95 \Omega`

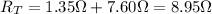
5. The 7.60 Ω and 1.70 Ω resistors are connected in parallel, and the 6.50-Ω resistor is connected in series with the parallel combination:
`7.89\Omega`

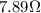
The total resistance of the two resistors connected in parallel is

`(1)/(R_T)=(1)/(7.60 \Omega)+(1)/(1.70\Omega)=0.720\Omega^(-1)\\R_T=(1)/(0.720 \Omega^(-1))=1.39 \Omega`

And the combination of these with the other resistor of 6.50-Ω in series gives a total resistance of

`R_T=1.39 \Omega+6.50 \Omega=7.89 \Omega`

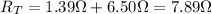
6. The 6.50 Ω and 7.60 Ω resistors are connected in series, and the 1.70-Ω resistor is connected in parallel with the series combination:
`1.52 \Omega`

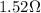
In this case, the total resistance of the two resistors in series is

`R_T=6.50\Omega + 7.60\Omega=14.10 \Omega`

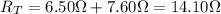
And the combination of these with the other resistor of 1.70-Ω in parallel gives a total resistance of

`(1)/(R_T)=(1)/(14.10 \Omega)+(1)/(1.70\Omega)=0.659\Omega^(-1)\\R_T=(1)/(0.720 \Omega^(-1))=1.52 \Omega`

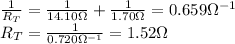
7. The 6.50 Ω and 1.70 Ω resistors are connected in series, and the 7.60-Ω resistor is connected in parallel with the series combination:
`3.94 \Omega`

In this case, the total resistance of the two resistors in series is

`R_T=6.50\Omega + 1.70\Omega=8.20 \Omega`

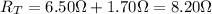
And the combination of these with the other resistor of 7.60-Ω in parallel gives a total resistance of

`(1)/(R_T)=(1)/(8.20 \Omega)+(1)/(7.6\Omega)=0.254\Omega^(-1)\\R_T=(1)/(0.720 \Omega^(-1))=3.94 \Omega`

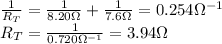
8. The 7.60 Ω and 1.70 Ω resistors are connected in series, and the 6.50-Ω resistor is connected in parallel with the series combination:
`3.83\Omega`

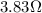
In this case, the total resistance of the two resistors in series is

`R_T=7.60\Omega + 1.70\Omega=9.30 \Omega`

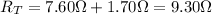
And the combination of these with the other resistor of 6.50-Ω in parallel gives a total resistance of

`(1)/(R_T)=(1)/(9.30 \Omega)+(1)/(6.50\Omega)=0.261\Omega^(-1)\\R_T=(1)/(0.720 \Omega^(-1))=3.83 \Omega`