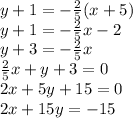Answer:
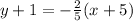
and
2x + 15y = -15
Explanation:
To write the point slope form, a point and a slope is required. Find the slope using the two points given and the slope formula.
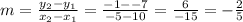
Substitute -2/5 and the point (-5,-1) into the form. Then convert to make the standard form of the equation.
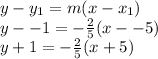
Now convert to standard form by applying the distributive property and moving terms.