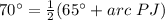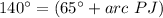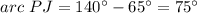Answer:
The measure of the arc PJ is
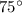
Explanation:
step 1
Find the measure of angle L
we know that
In a inscribed quadrilateral opposite angles are supplementary
so
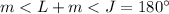
we have
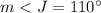
substitute
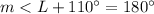
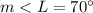
step 2
Find the measure of arc KJ
we know that
The inscribed angle measures half that of the arc comprising
so
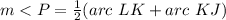
substitute the values
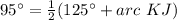
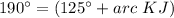
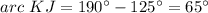
step 3
Find the measure of arc PJ
we know that
The inscribed angle measures half that of the arc comprising
so
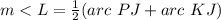
substitute the values