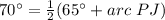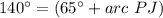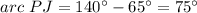Question

Given: circle k(O), m∠P=95°, m∠J=110°, m∠LK=125°
Find: m∠PJ

Answer 1

The measure of the arc PJ is
`75\°`

Explanation:

step 1

Find the measure of angle L

we know that

In a inscribed quadrilateral opposite angles are supplementary

so

`m<L+m<J=180\°`

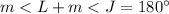
we have

`m<J=110\°`

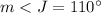
substitute

`m<L+110\°=180\°`

`m<L=70\°`

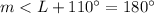
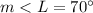
step 2

Find the measure of arc KJ

we know that

The inscribed angle measures half that of the arc comprising

so

`m<P=(1)/(2)(arc\ LK+arc\ KJ)`

substitute the values

`95\°=(1)/(2)(125\°+arc\ KJ)`

`190\°=(125\°+arc\ KJ)`

`arc\ KJ=190\°-125\°=65\°`

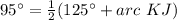
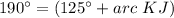
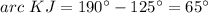
step 3

Find the measure of arc PJ

we know that

The inscribed angle measures half that of the arc comprising

so

`m<L=(1)/(2)(arc\ PJ+arc\ KJ)`

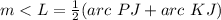
substitute the values

`70\°=(1)/(2)(65\°+arc\ PJ)`

`140\°=(65\°+arc\ PJ)`

`arc\ PJ=140\°-65\°=75\°`