Question

Which ordered pair (x, y) is a solution to the following system of equations?

{5x+4y=-14
{3x+6y=6

Answer 1

(-6, 4)

Explanation:

We are given the following two equations and we are to solve them:

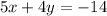`5x+4y=-14` --- (1)

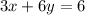`3x+6y=6` --- (2)

Using the substitution method:

From equation (2):

`3 x = 6 - 6 y \\\\ x = \frac { 6 - 6 y } { 3 } \\ \\ x = 2 - 2 y`

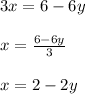
Substituting this value of x in equation (1) to get:

`5 ( 2 - 2 y ) + 4 y = -14 \\\\ 10 - 10 y + 4 y = -14 \\\\ 1 0 + 14 = 6 y \\\\ y = \frac { 24 } { 6 } \\ \\ y = 4`

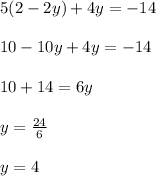
Putting this value of y in equation (2) to find the value of x:

`3 x + 6 ( 4 ) = 6 \\\\ 3x + 24 = 6 \\\\ 3x = 6 - 24 \\\\ x = \frac { -18 } { 3 } \\\\ x = -6`

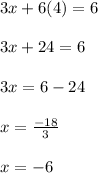
Therefore, (-6, 4) is the solution to the given system of equations.

Answer 2

Answer: (-6, 4)

Explanation:

You can use the Elimination method:

- Multiply the the first equation by -3 and the second one by 5.

- Add both equations.

- Solve for y:

`\left \{ {{(-3)(5x+4y=-14(-3)} \atop {5(3x+6y)=6(5)}} \right.\\\\\left \{ {{-15x-12y=42} \atop {15x+30y=30}} \right.\\-------\\18y=72\\y=4`

- Susbtittute y=4 into any of the original equations and solve for x:

`3x+6(4)=6\\3x=6-24\\3x=-18\\x=-6`

Then the ordered pair is:

(-6, 4)