Answer:
A total of zero softballs will fit into the container
Explanation:
step 1
Find the dimensions of the base of the prism
we know that
The volume of the prism is equal to

where
B is the area of the base
h is the height of the prism
In this problem we have
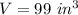

substitute in the formula and find the area of the base B
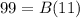
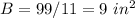
the length side of the square base is the square root of the area
so

we have that
The diameter of the softball 3.8 inches will fit (11/3.8=2.89 ) 2 times in the length of the container
The diameter of the softball 3.8 inches will fit 0 times in the width of the container
so
A total of 0 times of softballs will fit in the width of the container
therefore
A total of zero softballs will fit into the container