Answer:

Explanation:
The standard form of an equation of a circle:

(h, k) - center
r - radius
We have the end points of a diameter (8, 6) and (2, 0). The midpoint of a diameter is a center of a circle. Half of a length of diameter is a length of a radius.
The formula of a midpoint of a segment:
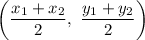
Substitute:

The center of a circle is (5, 3).
The formula of a length of a segment:

Substitute:
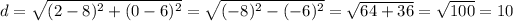
The length of a diameter is 10 units. The length of a radius r = 10 : 2 = 5 units.
Finally we have the equation of a circle:
