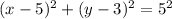Question

If the end points of the diameter of a circle are (8,6) and (2,0), what is the standard form equation of the circle

Answer 1

`\large\boxed{(x-5)^2+(y-3)^2=5^2\to(x-5)^2+(y-3)^2=25}`

Explanation:

The standard form of an equation of a circle:

`(x-h)^2+(y-k)^2=r^2`

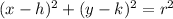
(h, k) - center

r - radius

We have the end points of a diameter (8, 6) and (2, 0). The midpoint of a diameter is a center of a circle. Half of a length of diameter is a length of a radius.

The formula of a midpoint of a segment:

`\left((x_1+x_2)/(2),\ (y_1+y_2)/(2)\right)`

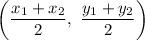
Substitute:

`x=(8+2)/(2)=(10)/(2)=5\\\\y=(6+0)/(2)=(6)/(2)=3`

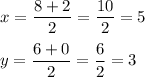
The center of a circle is (5, 3).

The formula of a length of a segment:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

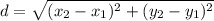
Substitute:

`d=√((2-8)^2+(0-6)^2)=√((-8)^2-(-6)^2)=√(64+36)=√(100)=10`

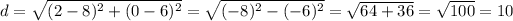
The length of a diameter is 10 units. The length of a radius r = 10 : 2 = 5 units.

Finally we have the equation of a circle:

`(x-5)^2+(y-3)^2=5^2`